Non interaction Fermi gas

无相互作用分布

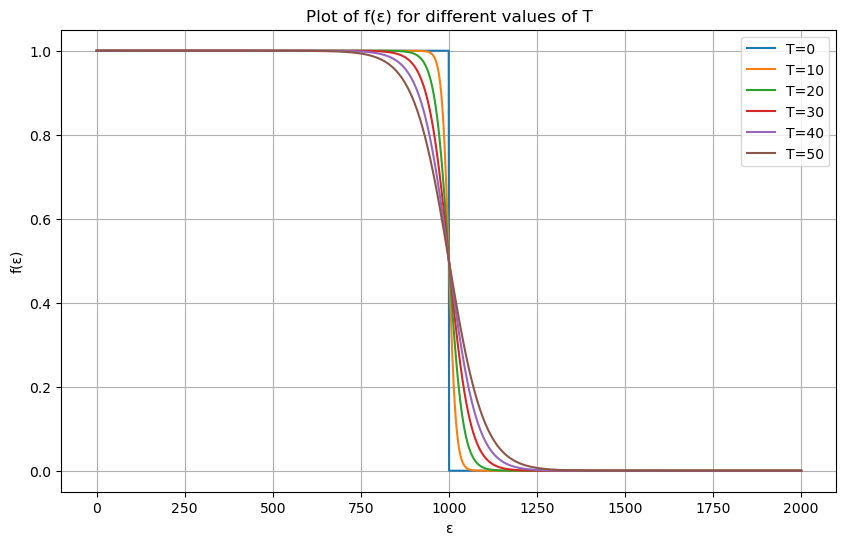由图可知，当$T=0$时，粒子全部处于费米面以下，有限温时，只有能量处于$k_BT$附近的粒子具有激发的可能。这源于泡利不相容。定义费米温度


1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
import numpy as np
import matplotlib.pyplot as plt

# Constants
mu = 1000
k_B = 1

# Function definition
def f(epsilon, T):
    return 1 / (1 + np.exp((epsilon - mu) / (k_B * T)))

# Epsilon values
epsilon_values = np.linspace(0, 2000, 2000)

# T values
T_values = [0, 10, 20, 30, 40, 50]

# Plot
plt.figure(figsize=(10, 6))

# Loop over T_values to create multiple lines
for T in T_values:
    # In the case T=0, to avoid division by zero, we will treat it as a special case.
    if T == 0:
        y_values = np.zeros_like(epsilon_values)
        y_values[epsilon_values < mu] = 1
    else:
        y_values = f(epsilon_values, T)
        
    plt.plot(epsilon_values, y_values, label=f'T={T}')

plt.title('Plot of f(ε) for different values of T')
plt.xlabel('ε')
plt.ylabel('f(ε)')
plt.legend()
plt.grid(True)
plt.show()

# Additional imports
from sympy import symbols, diff, exp

# Symbol definition
epsilon = symbols('epsilon')

# Function and its derivative
f_sym = 1 / (1 + exp((epsilon - mu) / (k_B * T)))
f_prime_sym = diff(f_sym, epsilon)

# Convert sympy expressions to numpy functions
f_np = lambda eps, T: np.array([float(f_sym.subs(epsilon, e).evalf()) for e in eps])
f_prime_np = lambda eps: float(f_prime_sym.subs(epsilon, eps).evalf())

# Calculate function value and derivative at the point of interest

T = 40
epsilon_0 = mu
f_value = f_np([epsilon_0], T)[0]
f_prime_value = f_prime_np(epsilon_0)

# Create tangent line values
tangent_line = lambda eps: f_prime_value * (eps - epsilon_0) + f_value

# Plot
plt.figure(figsize=(10, 6))
plt.plot(epsilon_values, f_np(epsilon_values, T), label=f'f(ε) at T={T}')
plt.plot(epsilon_values, tangent_line(epsilon_values), label='Tangent at ε=40')
plt.scatter([epsilon_0], [f_value], color='red')  # mark the tangent point
plt.title('Plot of f(ε) and its tangent at ε=40 for T=40')
plt.xlabel('ε')
plt.ylabel('f(ε)')
plt.ylim(0,1)
plt.legend()
plt.grid(True)
plt.show()

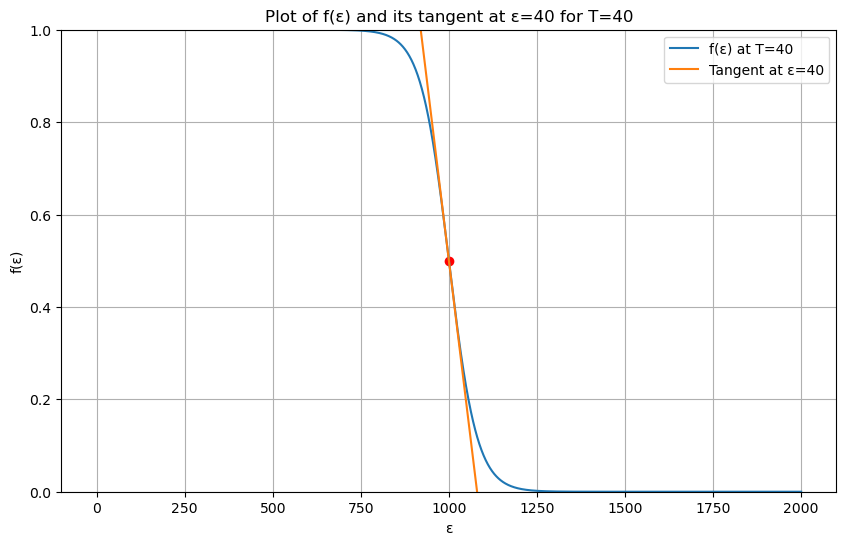
从图中看到，在靠近费米面附近，$f\propto \frac{1}{T}$

热容

动量空间中的电子态密度 $g(p)$

对于三维自由电子气体，能量-动量关系为 $E = \frac{p^2}{2m}$，其中 $p$ 是动量，$m$ 是电子质量。动量空间中的电子态密度 $g(p)$ 可以用以下方式表示：

其中 $V$ 是体积，$\hbar$ 是约化普朗克常数。

从动量态密度$g(p)$ 到能量态密度 $g(E)$

能量和动量的关系为 $E = \frac{p^2}{2m}$。我们可以通过链式法则得到：

于是，能量态密度 $g(E)$可以通过以下方式从 $g(p)$ 获得：

计算内能 $U$

这个积分需要数值方法或者特殊函数来解决。但在高温和低温极限下，有解析解。

三维自由电子气体的热容量：低温极限

费米分布函数在低温极限的线性化

在低温极限下$(T/ T_F)$，只有接近费米面的电子态被热激发。在这种情况下，费米分布函数 $f(E)$ 可以线性化为：

内能 ( U ) 的变化

内能 $U$ 在 的值为 $U_0$，它主要来自 $E < \mu$ 的电子。由于只有接近费米面的电子被激发，$\Delta U = U - U_0$可以用以下形式近似：

因此，低温下的热容 $C$ 与 $T$成线性关系，即 $C \propto T$。

电导率

自由电子气体的电导率与 $T^2$ 的关系

Drude 模型

电导率 $\sigma$ 可以用 Drude 模型进行描述，该模型在包括电子散射的情况下给出：

其中：

  • $n$ 是电子密度
  • $e$ 是电子电荷
  • $\tau$ 是电子的弛豫时间（或散射时间）
  • $m$ 是电子质量

弛豫时间 $\tau$

弛豫时间 $\tau$ 是一个关键的参数，它反映了电子与其他电子或晶格声子的散射过程。在低温下，$\tau$ 主要受到电子-电子散射的影响，这一过程可以通过费米黄金规则来描述。

低温下的 ( T^2 ) 关系

在低温极限下，只有接近费米面的电子会参与散射过程，因为只有这些电子有可用的空态可以跃迁。这意味着弛豫时间 $\tau$ 将与温度的平方 $T^2$ （注：激发态处于正的$T$范围，空穴态在负的$T$范围，散射通道的态密度正比于$T$，故需要满足平方关系）成正比。

具体来说，弛豫时间 （$\tau$）可以表示为：